[선형대수학] System of Linear Equations
System of Linear Equations
선형대수학(Linear Algebra) 같은 경우는 영어로 배우는 것이 낫다고 생각되어 여기서 사용하는 단어는 모두 영어를 사용할 예정이다. 설명은 한국어로 하겠지만, 단어와 주제는 모두 영어이다.
Linear Equation
먼저 Linear Equation에 대한 설명이 필요하다. 흔히 우리가 알고 있는 1차 방정식을 일컫는다. Linear Equation을 공식화하면 다음과 같다.

위의 식에서 a1, a2, ... , an, b 등은 coefficients라고 한다. 우리가 흔히 알고 있는 계수라고 생각하면 된다. n의 갯수는 양의 정수로 얼마든지 커질 수 있다. 책에서는 2~5 정도의 크기로 나오지만, real-life에서는 50개나 5000개와 같이 훨씬 커지는 경우가 많다.
예시를 한번 확인해보자 아래의 식들이 Linear Equation인지 확인해보자.


예시1)의 경우 Linear Equation임을 확인할 수 있다. 하지만 예시2)의 경우 x1x2가 곱해져 있거나, 루트 x1이 존재하는데 이때는 Linear Equation이라고 할 수 없다.
System of Linear Equation
우리는 연립방정식이라는 개념을 이미 알고 있다. 이것을 Linear Equation에 적용한 것이 System of Linear Equation이다. 혹은 Linear System이라고 부른다. 공식적인 정의는 Linear Equation의 Collections이고 같은 변수들을 포함하고 있어야 한다. 아래는 Linear System의 예시이다.

당연하게도 이 System에는 정답이 존재한다. 예를 들어 위의 식에 (5, 6.5, 3)을 대입해보면 정답인 것을 확인할 수 있다. 가능한 정답의 모든 집합을 Solution Set이라고 한다. 그리고 두 Linear System의 Solution Set이 같다면 Equivalent 하다고 한다.
Linear System한 예시를 들어보자.

위의 식은 전형적인 Linear System 문제인데 그래프로 보면 두 직선의 교점을 구하는 것과 같음을 우리는 이미 알고 있다. 그렇다면 이것 또한 당연해진다. 직선은 한 점에서 만나거나, 평행하거나, 일치할 수 있다. 결국 Linear System의 Solution은 다음과 같은 성질을 같는다.
System of Linear Equation은
1. 정답이 없거나
2. 정답이 하나거나
3. 정답이 무수히 많다.
정답이 하나거나 무수히 많은 경우, 즉 정답이 하나라도 있는 경우에는 consistent라고 말한다. 정답이 없는 경우에는 반대로 inconsistent라고 말한다.
Matrix Notation
우리는 앞에서 배운 Linear System을 Matrix로 표현할 수 있다. Matrix는 행렬을 의미한다. 예시를 통해 살펴보자.

위의 식은 흔히 아는 Linear System이다. 각각의 Linear Equation의 coefficients를 Matrix 값에 넣는 것이다. 그렇다면 아래와 같이 표현할 수 있다. 이를 Coefficient Matrix라고 한다.
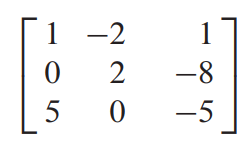
하지만 여기에는 b에 해당하는 것은 포함되어 있지 않다. 그렇기에 우리는 Augmented Matrix를 정의한다.

오른쪽에 b에 해당하는 coefficients가 생긴 것을 확인할 수 있다. 저렇게 오른쪽에 띄어서 쓰기도 하고 바를 긋는 경우도 있다.
Solving a Linear System
우리는 이제 Linear System의 Solution을 구해볼 것이다. 문제를 푸는 것은 간단한데, 각 row마다 변수 1가지만 남겨두고 다 값을 0으로 만드는 것이 목표다. 각 Linear Equation을 다른 Linear Equation에 곱하고 더해서 값을 변화시킬 수 있다. 그래서 변수 1개만 값을 남기고 모두 0으로 만들어볼 것이다. 이것이 이해가 어렵고, 왜 하는지도 모르겠다면 예제를 확인하는 편이 빠르다.
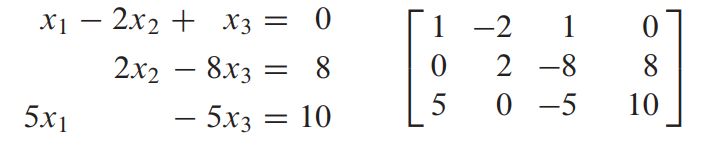
앞에서 소개했던 식을 그대로 사용할 것이다. 먼저 첫 번째 row의 경우 x1의 coefficient가 1인 것을 확인할 수 있다. 이것을 기준으로 하여 나머지 row에서는 x1 값이 존재하지 않도록 없애준다. 두 번째 row는 이미 0이고 세 번째 row는 5의 값이 있으니 첫 번째 row에 5를 곱해서 3번째 row에 빼주면 0이 된다.

이렇게 세번째 row가 변하게 되면 다시 Matrix에 넣는다.

이번에는 두번째두 번째 row에서 x2를 기준으로 해서 다른 row에는 값이 없도록 만들어줄 것이다. 이때 두 번째 row는 자신보다 아래에 있는 것부터 해결한다. 이유는 나중에 설명하도록 하겠다. 먼저 coefficient가 1이 되도록 두 번째 row를 2로 나눠준다.

그리고 두번째 row에서 10을 곱하고 3번째 row에 빼준다.

나온 결과를 30으로 나누고 다시 Matrix에 넣어준다.
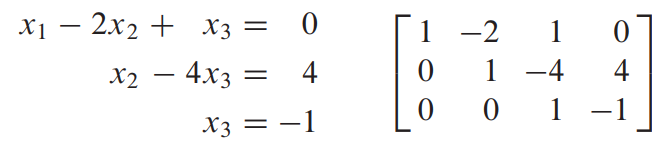
이렇게 되면 1차적인 작업은 끝이 난다. 지금만 해도 답을 구하기 쉽지만, 제대로 구하기 위해서는 나머지 오른쪽 대각선 값들도 0으로 만들어준다. 이번엔 반대로 x3부터 시작해서 1,2번째 row의 x3 값들을 0으로 만들어준다.
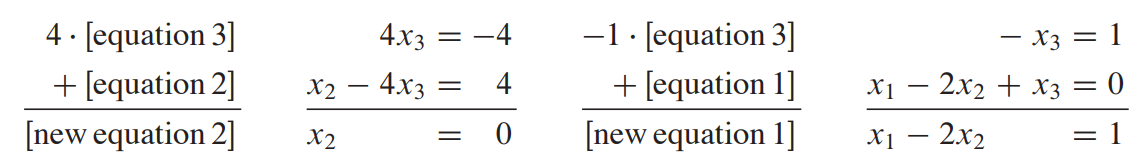
위와 같이 계산하면 다시 Matrix를 아래와 같이 적을 수 있다.

그리고 이제 마지막으로 row에서 2를 곱해서 row1에 더해주면 row1에 있던 x2 값도 사라지게 된다.

이렇게 결과가 나오면 정답을 도출한 것이다. x1=1, x2=0, x3=-1이 정답이다. 따라서 (1, 0, -1)이 System의 Solution이라고 할 수 있다.
이러한 방식을 정리한 Elementary Row Operations가 있다.
1. 한개의 row를 다른 row의 곱하고 더한 형태의 row로 바꿀 수 있다. (Replacement)
2. 두개의 row의 위치를 바꿀 수 있다. (Interchange)
3. 0을 제외한 값을 row에 곱할 수 있다. (Scaling)
이 Row Operations를 통해 한 개의 Matrix가 다른 하나의 Matrix를 만들 수 있다면, 이 두 Matrix는 Row Equivalent하다고 말한다.
Existence and Uniqueness Questions
수학에서는 항상 정답이 존재하는지, 고유한지를 묻고 싶어 한다. 이것이 바로 Existence와 Uniqueness다. 우리에게 Augmented Matrix가 주어졌을 때, 이 System이 consisten인지(해가 존재하는지), 해가 존재한다면 unique한지(해가 1개만 존재하는지) 질문할 수 있다. 이를 확인하는 방법은 다음 섹션에서 더 자세히 하겠지만 지금은 예시를 통해서 확인해보자.

위에서 보았던 식을 다시 사용한다. Row Operation을 통해서 정리하면 중간에 다음과 같은 결과를 얻을 수 있었다.

이 경우 이미 이 상태에서 x3가 확정되었고, 결국 자동적으로 x2와 x1값이 나올 수 있다. 그러므로 해는 존재하고(Existence), 값도 고유(Uniqueness)하다. 하지만 다음과 같은 예시는 어떨까?

앞에서 풀이를 많이 해봤으므로 중간 풀이는 생략하겠다. 다들 직접 손으로 풀어보기를 바란다. 여기서는 두 번째 row와 첫 번째 row의 위치를 바꾸는 것이 중요하다. 그렇게 이 System을 Row Operation으로 풀게 되면 다음과 같은 Matrix를 얻는다.

즉, Linear System으로 바꾸면 아래와 같은 식이 나온다.
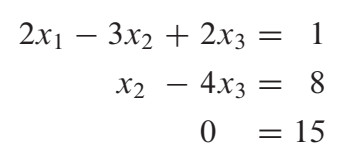
0 = 15라는 것은 당연히 정답이 될 수 없다. 따라서 이 Linear System은 정답이 존재하지 않는다. 이를 그림으로 이해하면 다음과 같다.

세 개의 평면이 만나는 한 점이 존재하지 않는 것이다.
이렇게 Linear System에 대한 기본적인 내용을 알아보았다. 선형대수학은 모든 분야에 쓰이고 공학의 기본이 되는 수학이기에 제대로 공부할 필요가 있다. 선형대수학은 문제 풀이보다 눈으로, 머릿속으로 그림을 그려 이해하는 것을 추천한다. 그렇다면 선형대수학을 적용할 수 있는 무궁무진한 가능성을 볼 수 있을 것이다.
참고 문헌: Linear Algebra and Its Applications