합성함수 미분법
우리는 고등학교 시절에 합성함수 미분에 대해 배운 적이 있다. 그때는 x에 대한 미분만 정의하였지만, 여기서는 다변수 함수에서의 합성함수 미분을 정의할 예정이다.
연쇄 법칙(Chain Rule)
이변수함수 f(x, y)의 편미분이 모두 연속이고 변수 x와 y가 열린 구간 I에서 정의된 t의 함수로서 각각 미분가능할 때, f(x, y)=f(x(t), y(t))는 t의 함수로서 t에 관해 미분 가능하며 아래와 같은 식을 얻는다.

x(t)와 y(t)를 X(t)로 바궈서 일반화를 시켜보자.
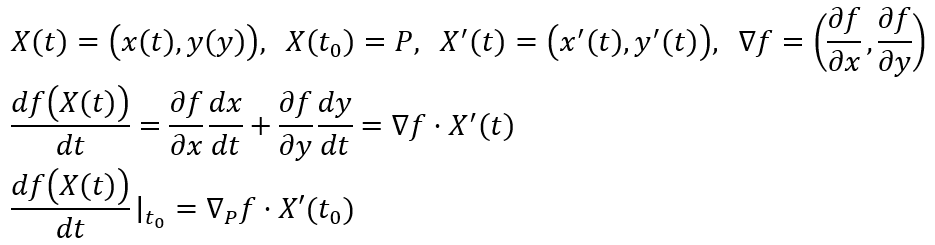
연쇄법칙은 X(t)라는 곡선을 따라서 변수가 움직일 때 f의 평균 변화율을 구하는 것이다. 아래 예제를 통해 확인해보자. 곡선 y=x^2를 따라 P=(2,4)로 접근하는 경우 P에서의 z=f(x, y)=x^2+y^2의 순간 변화율을 구해보자.

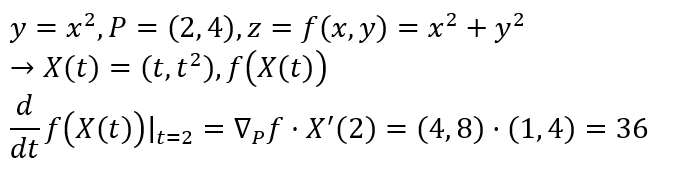
X(t)를 다음과 같이 정의할 수 있고, t=2일 때 P=(2, 4)에 도달하므로 2에서의 미분을 구하면 된다.
합성함수 미분법을 배웠으므로 이전에 배웠던 방향미분이 기울기 벡터와 v와의 내적임을 쉽게 증명할 수 있다. X(0)=P를 지나고 X'(0)=v와 평행한 직선의 매개변수식을 X(t)로 두면 아래와 같이 증명이 가능하다.
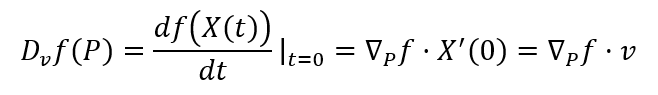
음함수 정리
미분가능한 함수 f의 등위선 f(x, y)=c 위의 한 점 P=(x, y)에서 fy가 0이 아니면 P를 포함하는 열린 원판이 있어 y가 x의 함수로서 미분 가능하고 아래 식을 만족한다.
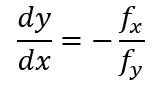
이를 통해 함수의 등위선과 기울기 벡터가 수직임을 알 수 있다. 음함수 정리를 증명하는 방법은 아래와 같다.

음함수 정리를 삼변수의 경우에 정의할 수 있다. 삼변수함수 w = f(x, y, z)의 한 등위면 f(x, y, z)=c에서 z가 x와 y의 함수로서 미분 가능하면 아래의 식을 만족한다.

이를 증명하는 방법은 다음과 같다. 먼저 한 점에서 x,y에 대한 z의 식을 구성하고, 접평면의 식을 이용한다.

zy는 같은 방법으로 증명하면 된다.
이 방법을 통해 등위면을 정의하여 접평면을 구하는 문제들을 쉽게 해결할 수 있다.
참고 문헌: 반전학습을 위한 다변수 미적분학(경문사)
'Mathematics > Calculus' 카테고리의 다른 글
| [Calculus] 라그랑주 승수법 (Lagrange Multiplier Method) (2) | 2022.08.22 |
|---|---|
| [Calculus] 다변수함수의 최대 최소 (0) | 2022.08.18 |
| [Calculus] 방향미분과 미분가능성 (2) | 2022.08.08 |
| [Calculus] 접평면과 근사식 (0) | 2022.08.07 |
| [Calculus] 편미분 (0) | 2022.08.06 |




댓글